
みる子さーん、トイレットペーパーが品薄で、近所のドラッグストアでどこも「入荷未定」ですよー(泣)。
新型コロナウィルスのせいでトイレットペーパーが不足するってデマのせいで、買い占め騒動が起きてます。

本当にひどい状況だな。オイルショックの時からまるで成長していない。生活必需品の備蓄が尽きた人は、実に苦労していると思う。
だが、一般家庭のトイレットペーパーの消費量は通常変わったりしないので、いずれ在庫は回復するだろう。
もう少しの辛抱だから、慌てず落ち着いて、理性的に行動してほしい。

うーん……困った……もう家に備蓄がないです……。

お店や公衆トイレからパクったりするなよ。

しませんよ、そんなの……。
でも、どうしてこんなことが起こってしまうんでしょう?

普段と同じく、全員が自分の必要な分だけ買っていれば、在庫が不足するなんてことは無いが、消費者はそのように社会的に最適な行動をとることができない。
こういった状況を説明するのに「囚人のジレンマ」という経済学のゲーム理論の考え方がある。

ゲーム理論ですか?
ゲーム理論
囚人のジレンマ

「囚人のジレンマ」とは経済学のゲーム理論における用語の一つだ。
個々人が己の利益のみを追求し、協力関係を作らない(=裏切った)方が利益が得られるケースが存在する場合、協力関係を作る方が利得が大きいと分かっていても、裏切る方を選択してしまうというジレンマだ。

うーん……?難しいですね。

具体的に説明しよう。
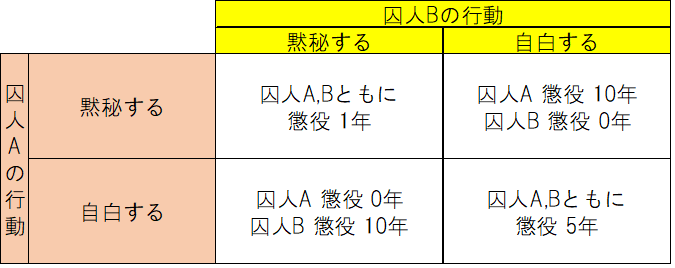
共犯関係である囚人A、Bが居て、それぞれ別室で取り調べを受けているとする。
・A、Bともに黙秘した場合、双方に懲役1年が課せられる。
・どちらかが自白した場合、自白した方は釈放、しなかった方は懲役10年が課せられる。
・A、Bともに自白した場合、双方に懲役5年が課せられる。

おー、なるほど。
A、Bで協力して黙秘するか、それとも自白して自分だけ懲役0年になるか……。
でもどっちも自白してしまったら懲役5年ですか。

その通り。
そして、このケースでは裏切った方が懲役を免れるケースがあるので、囚人は協力をしなくなる、というジレンマだ。

ああ、囚人Aにとってみれば、Bが黙秘したとしたら懲役1年(A黙秘)または懲役0年(A自白)なので自白しちゃう方がお得であると。
同じく、Bが自白したとしたら懲役10年(A黙秘)または懲役5年(A自白)ですからやっぱりAは自白した方が得をすると。
自分の利得だけを考えた時に、協力せずに自白、つまり裏切った方が良いわけですね。

察しが良いな、その通りだ。
さて、これを今回の騒動に当てはめてみよう。

おおー。
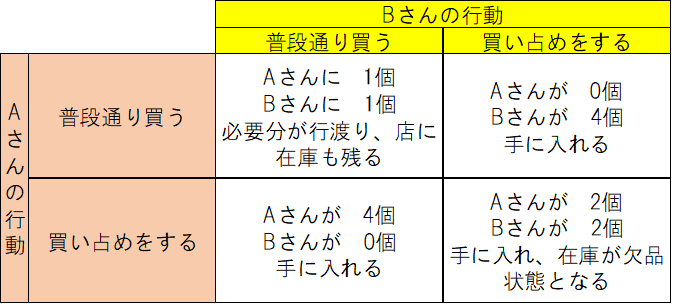
これだと確かに、「普段通り買う」という戦略を選択した時に、生活必需品が0個という結果になってしまいますから、皆が買い占めに走るわけですね。

Aさんにとっては、Bさんがどのような戦略を選択した場合でも、「買い占めをする」方が有利となる。その逆も同様だ。どのようなケースでも有利となる戦略の事を「支配戦略」という。
ナッシュ均衡

相手プレイヤーの戦略がわかっていたと仮定する。
自分の戦略を変えることでより大きな利得を得るケースがあるのならば、自分の戦略を変えるはずだ。
そして、どのプレイヤーも、どのように戦略を変えてもそれ以上利得が高くならない戦略の組み合わせを、ナッシュ均衡という。

えーと……例えばこんな感じですね。
Bさんが普段通り買うと仮定した場合、Aさんが最も高い利得を得ようとするならば、買い占めをすることを選びますよね。
で、Aさんが買い占めをする場合はBさんも買い占めをする方が利得が高くなるわけですから、買い占めをすることを選ぶと。
お互いに「買い占めを選んでいる」状態がナッシュ均衡というわけですね。自分の戦略を変えてもそれ以上利得が高くならないわけですから。

「囚人のジレンマ」状態ではナッシュ均衡は一つとなる。
一方、ナッシュ均衡は複数同時に存在することもある。
例えば以下のようなケースだ。
A君はフレンチに行きたいが、Bさんと一緒に食事をする方が大事と考えている。
Bさんはイタリアンに行きたいが、A君と一緒に食事をする方が大事と考えている。

この場合のナッシュ均衡は二人が一緒に食事をすること、つまり「ABともにフレンチを選ぶこと」または「ABともにイタリアンを選ぶこと」の2つが存在する。
・A君がフレンチを選ぶ時、Bさんはイタリアンを選ぶ方が利得が低くなる。
・A君がイタリアンを選ぶ時、Bさんはフレンチを選ぶ方が利得が低くなる。

つまり、プレイヤーが異なるレストランを選んでいる状態では、戦略を変更した方が利得が高くなるので、それはナッシュ均衡ではない。
同じレストランを選んだ場合は戦略を変更すると利得が低くなるので、ナッシュ均衡と言える。

ナッシュ均衡では、どのプレイヤーも戦略を変える必要がないんですね。
パレート改善

ある資源配分状態、例えば今回で言うとトイレットペーパーがどう分配されているかだが、Aさんの効用が下がることなくBさんの効用を上げることが出来る状態へ変化させることを、パレート改善という。

効用って何ですか?

財やサービスを得るときの満足感のことだ。

なるほど。
たとえばトイレットペーパーで言ったら、「Aさんが4個・Bさんが0個」の状態から、「Aさんが2個・Bさんが2個」という状態にするのは、パレート改善と言えますよね?

お、よくわかったな。

だって普段は定期的に1個ずつしか買わないトイレットペーパーを、同時に3個も4個も持っていても、効用(満足感)は変わらないわけですよね。だったらAさんの2個をBさんに分配することで、Aさんの効用を下げることなくBさんの効用を上げることが出来ます。

その通りだ。
さらに、今回の仮定でいうと、必要分の補充というのは「定期的に1個ずつ買う」というものだ。
つまり、1個持った時点ですでに効用は最大化されている。1個が2個になったとて、効用の上がり幅はゼロなわけだ。

分配状況がAさん1個・Bさん1個の時点で、すでに社会的な資源配分としては最適なわけですね。

パレート改善がそれ以上なされない状態のことを「パレート最適」という。
ナッシュ均衡は個々人が最適な戦略を取った末に辿り着く状態だが、それが必ずしもパレート最適に辿り着くわけではない、というわけだ。
補足:限界効用について

効用関数というものがあり、財の増減と効用(満足度)の変化量を表した曲線の事だ。
一般的には、財が多ければ多いほど効用が上がると考えられ、右上がりの曲線として描かれる。


グラフの青線が効用関数なんですね。
でも途中からだんだん、効用が上がらなくなってきますね。

与えられる財が多くなるほど、だんだん嬉しくなくなってくる、と言う考え方だな。

チョコレート10個貰ったら嬉しいですけど、20個貰うときとそんなに嬉しさが変わらない、って感じですか。

そうした効用の上がり度合(2点間の傾き)のことを「限界効用」と呼ぶ。
図でいうと限界効用①つまり財が0個から10個に増えるときは傾きが大きいものの、限界効用②つまり財が10個から20個に増えるときの傾きは小さくなっている。

なるほど。個数が多くなるほど、限界効用は下がるわけですね。
さっきのトイレットペーパーも同じで、1個も2個も効用が変わらないなら、社会的に多くの人に分配されるようにした方が良いですよね。
冷静に、理性的に、行動しましょう

というわけで、経済学の理論について紹介してみた。

勉強してみるとけっこう面白いです。

経済学は中小企業診断士試験の一科目でもあるが、今回紹介したようなことは、そこでも詳しく勉強することが出来るぞ。経済学を押さえておくと、社会が見えるな。

そうかもしれませんね。
皆さんも落ち着いて行動して、誰かが困ることのない戦略を選べれば良いですね。

そういうことだ。それでは今日はここまでだ。

ありがとうございました。







