商品や製品の売れ行きの過去データを蓄積し、それをもとに将来の必要量を計算する需要予測。
正確な需要予測が可能となれば、それは市場を支配したのと同義であり、需要予測はビジネスにおいて重要な役割を持つ。
今回は数理的なモデルにより将来の需要を計算する基本的な手法について(可能な限り平易に)ご紹介する。
はじめに:需要予測の意義
多くの場合、需要予測は、企業内の経験豊富な担当者が「職人技」的に業界動向を見極めつつ、数理的計算を用いるまでもなく将来の需要計画を立てているのが実態なのではないだろうか。
人間が様々な情報を懸案し需要計画を立てるか、数理モデルにより需要計画を策定するのか。
これらは「どちらを選択すべきか」という次元のものではない。
よくシステム導入の現場で数理モデルベースの需要予測機能を実装しようというときに、「これって良く当たるの?」と訊かれることがある。
しかし、需要予測の意義とは「当たる」とか「当たらない」といった次元にあるのではない。
(精度は確かに重要なのだが、宝くじとはちがうので)
人間が優れた感性で需要を見極めようが、優れた数理モデルを用いようが、そもそも未来を完全予測することなどできない。
重要なのは、根拠に基づき予測を行い、それと実績がズレた場合は何が原因だったのかを考え、次回の予測をより精度の高いものにしていくというアプローチを繰り返すことだ。
システム的な需要予測であったり、数値的根拠に基づく予測というのは、そうしたサイクルを回す際の指針として活用するためのものというわけだ。
需要予測の基本的手法
需要予測は過去のデータに基づいて行う。
その際に重要なのが、過去のデータにどう「重みづけ」を行うかだ。
10年前のデータと直近のデータを、同等に扱っても良いのだろうか?
通常は、あまりにも古いデータでは参考にならないことが多いし、一方で10年前程度であれば同等に考慮すべき、というケースもある。
つまりケースバイケースで選択すべきモデルも異なってくる。
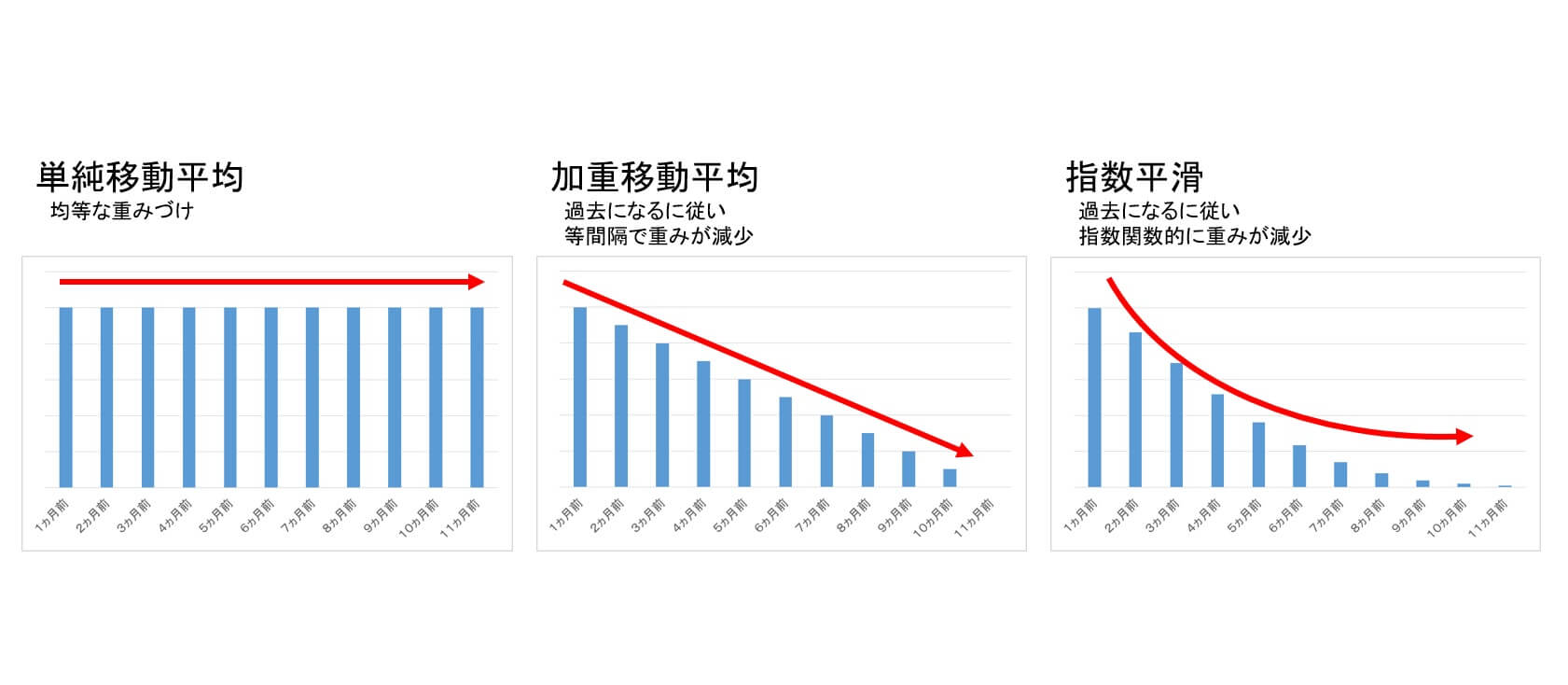
今回は「単純移動平均法」「加重移動平均法」「指数平滑法」について順に解説する。
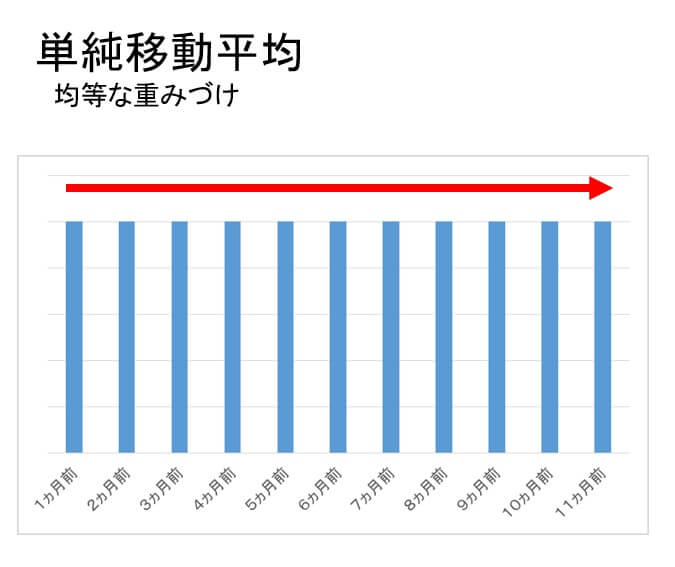
単純移動平均法とは
単純移動平均はデータの重みづけが平坦な平均であり、過去のデータも直近のデータも同等に扱う。過去の実績値全部を合算して、期間で割ることで求められる。
もっともわかりやすい方法と言える。
加重移動平均法とは
過去になるに従い、重みを等間隔で減少させていく平均方法が加重移動平均。直近のデータほど重く扱う。
加重平均の係数(0以上1以下)として、例えば前月に対して最大値1の重みを付け、そこから1か月遡るごとに重みを0.1ずつ減少させていくとする。
係数は10か月遡れば0となる。
よってこのケースでは、過去10か月分のデータが重みを付けて考慮されるし、それより以前の月に関しては切り捨てられることとなる。

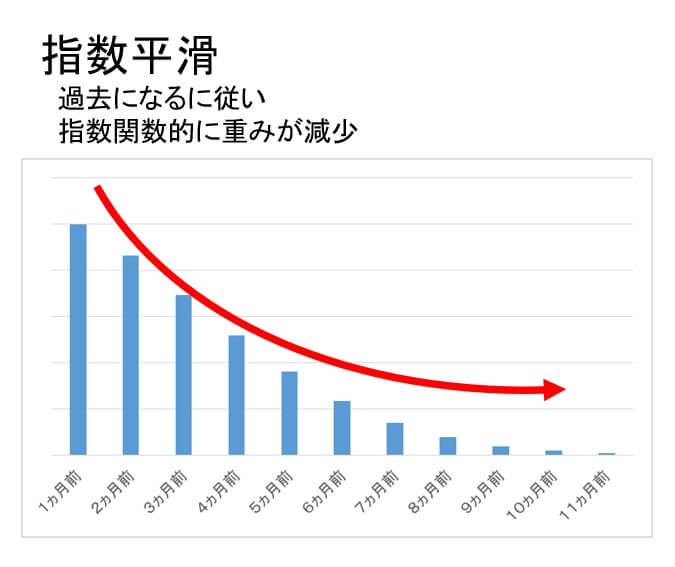
指数平滑法とは
指数平滑とは、過去の実績データを用いつつ「より新しい方の実績値」により大きな重みを置き、過去になるほど小さな重みをかけて移動平均を算出するもの。
①過去に遡るほど、重みは指数関数的に減少するので「指数」平滑と呼ばれている。
②単純移動平均は、過去データのすべてを同じ重みで扱うのに対し、指数平滑法は直近のデータほど重視して扱う。
③加重移動平均は、過去の重みがある時点で0となるので、それより以前のデータは考慮されない。一方、指数平滑は過去に遡っても重みづけが0になることはなく、過去データのすべてを予測値に反映する。
指数平滑の計算式
計算式は下記の通り。
今期の指数平滑値 = 1期前の指数平滑値 + α係数(1期前の実績値 – 1期前の指数平滑値)
1期前の実績値と、1期前の指数平滑値の差に重み(α係数)をかけて、1期前の指数平滑値に加えた数値を、今期の指数平滑値とする。
今期の指数平滑値 = α(1期前の実績値) + (1 – α)(1期前の指数平滑値)
⇒この形の式も覚えておくと、後述の式も理解しやすい
平滑化定数αとは
平滑化定数αは、0以上1以下で定義される係数。
αが1に近いほど直近のデータが重視され、αが0に近いほど過去のデータが重視される。
需要が不安定な場合はαを1に近づけ、安定的である場合はαを0に近づける。
ではα係数は任意の数値で良いのかというと、最適値を求める手法がある。
最適値は需要実績値と予測値の平均絶対偏差(MAD:Mean Absolute Deviation)が最小になるように求める。
要するに、実績値と予測値の間の差を絶対値で平均を取り(「両者の数値がどれだけ離れているか」の平均)、需要予測を適用する過去データの期間内において、これが最小となる(要するに実績と予測の乖離が少ない)αの値を求めるということ。
要するにと言いつつあまり要約できた気がしないが、詳しくは専門書にあたっていただきたい。
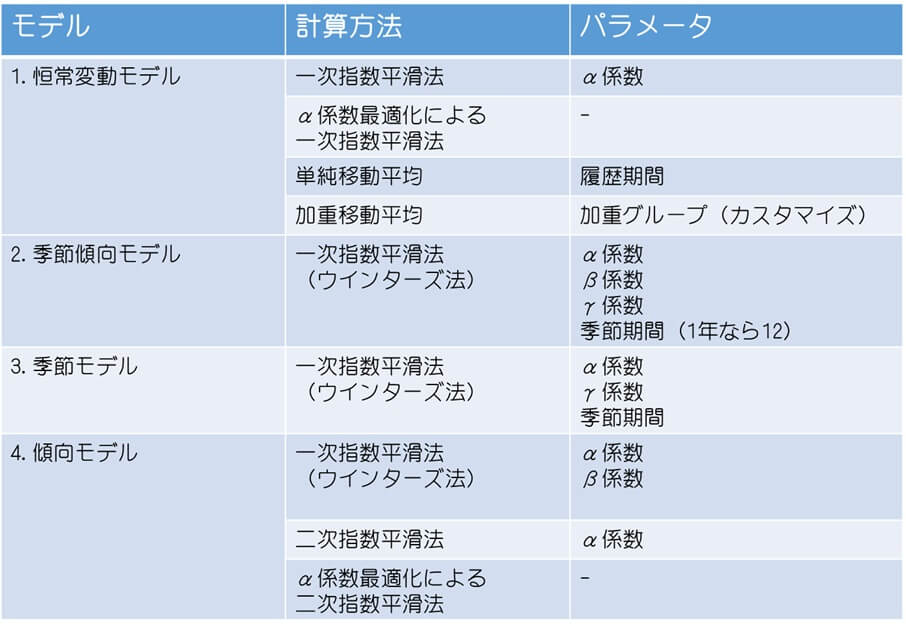
ウインターズ法(季節傾向モデル)
ウインターズ法による需要予測は、季節によって変動する需要や、長期的な増加や減少傾向を需要予測値に反映させる指数平滑法を用いた手法だ。
季節変動を考慮する季節モデル、傾向を考慮する傾向モデル、その両方を考慮する季節傾向モデルといったものがある。
<季節傾向モデルの計算式>
指数平滑を利用して基準値、傾向値(トレンド)、季節変動値の3要素を用いて計算する。
また、先述の平滑化定数αに加え、β係数(トレンド係数)、γ係数(季節変動係数)が登場する。
次期需要予測 = (今期の基準値 + 今期の傾向値) × (1周期前+1期の季節変動値)
【基準値、傾向値、季節変動値の計算】
今期の基準値 = α(今期の実績 ÷ 今期の季節変動値) + (1 – α)(前期の基準値 + 前期の傾向値)
今期の傾向値 = β(今期の基準値 – 前期の基準値) + (1 – β)(前期の傾向値)
今期の季節変動値 = γ(1周期前の実績 ÷ 1周期前の基準値) + (1 – γ)(1周期前の季節変動値)
このように3つの要素を合成することにより、トレンドと季節傾向を加味した需要予測値を求めることが出来る。
ロジスティクス分野の専門知識(おススメ参考書)
ロジスティクス分野で専門知識にあたりたい時は、『ロジスティクス工学(経営科学のニューフロンティア)』がおススメ。
以下のようなテーマを数学的・工学的に体系化して説明している。
・発注モデル
・配送計画モデル
・動的ロットサイズ決定モデル
・スケジューリングモデル
・ロジスティクスネットワーク設計モデル
他多数
数式が多数登場する専門的な内容で難易度も高く、通読目的というよりは、特定のロジ分野で専門的な知識や工学モデルにあたりたいときに活用できる。