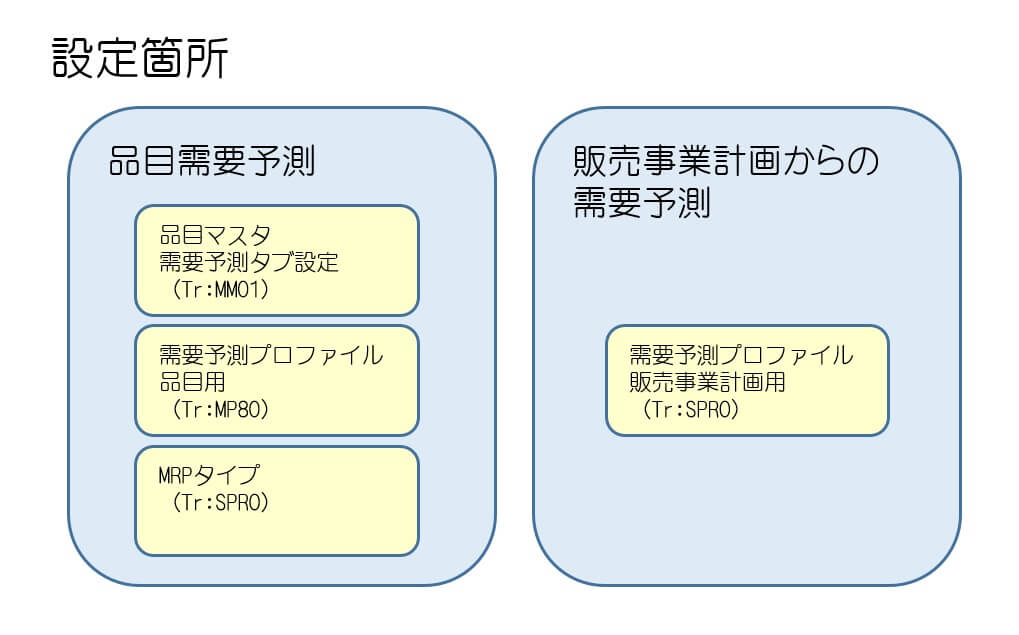
SAPでは主に4つの需要予測モデルから、各品目や販売事業計画ごとに、どのモデルを適用するかを選択することが出来る。
・恒常変動モデル
・季節モデル
・傾向変動モデル
・季節傾向モデル
今回はこれらのモデルについて、計算方法や実行時に指定するパラメータについて解説する。
なお、需要予測モデルの理解には、指数平滑法およびそれを用いたウインターズ法の理解が前提となる。詳しくは以下の記事で解説しているので、先に参照頂きたい。

需要予測モデルの解説
需要予測実行はいくつかの機能から可能だが、今回は販売事業計画(Tr:MC87)から需要予測を実行する際の入力画面を例に説明する。
販売事業計画(Tr:MC87)では、需要予測を実行する際、メニューの【編集 >販売計画登録 >需要予測】を選択する。
すると、需要予測期間の指定(需要予測を行う未来の期間、および過去実績データとして参照する期間)および、どの需要予測モデルを適用するか選択する画面が現れる。
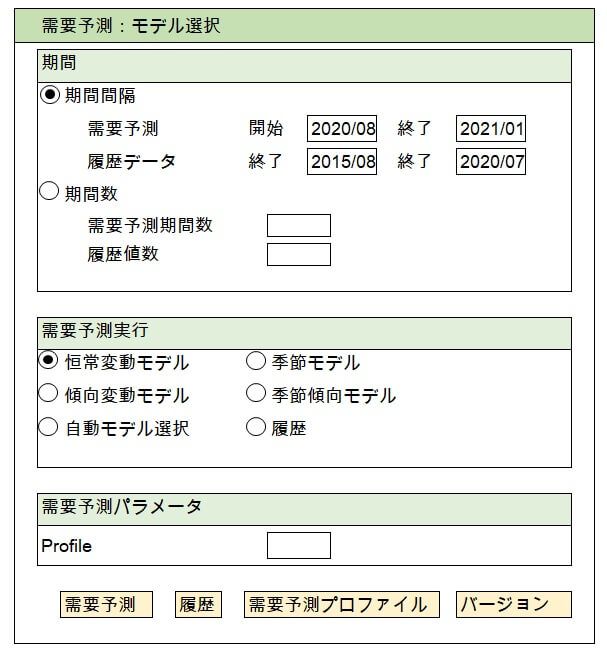
「需要予測実行」のグループボックスにあるとおり、4つの需要予測モデルが選択できる。(自動モデル選択及び履歴の説明は割愛)
いずれかの需要予測モデルを選択し、「需要予測」ボタンを押すことで、各需要予測モデルにおける計算方法を選択、および計算パラメータを入力する画面が現れる。
選択・入力項目は、各モデルごとに以下の通りとなっている。
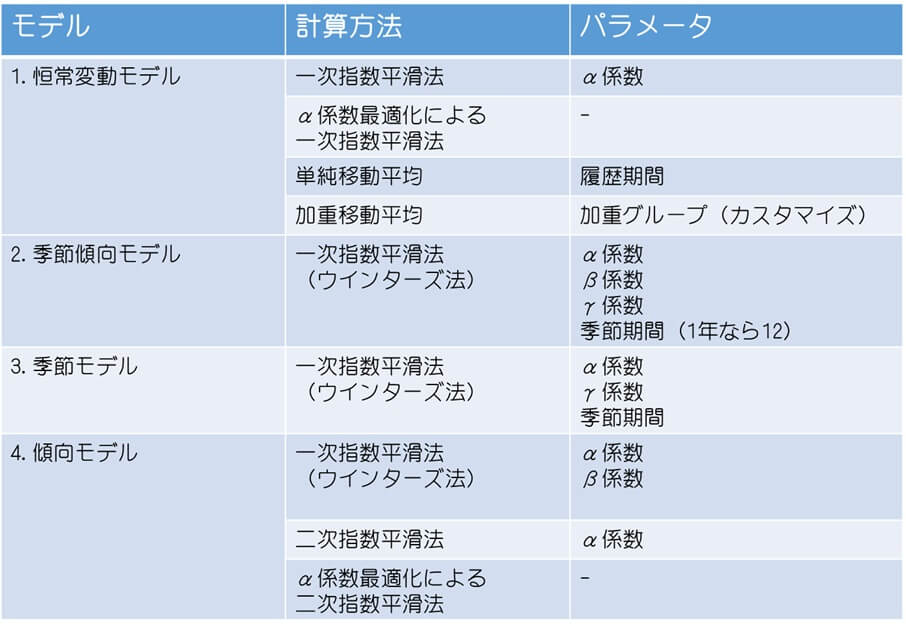
ここから、各モデル・計算方法および計算パラメータの意味について解説する。
恒常変動モデル
恒常変動モデルは、需要量が季節的・傾向的に変化しない場合に適用する。
一次指数平滑法
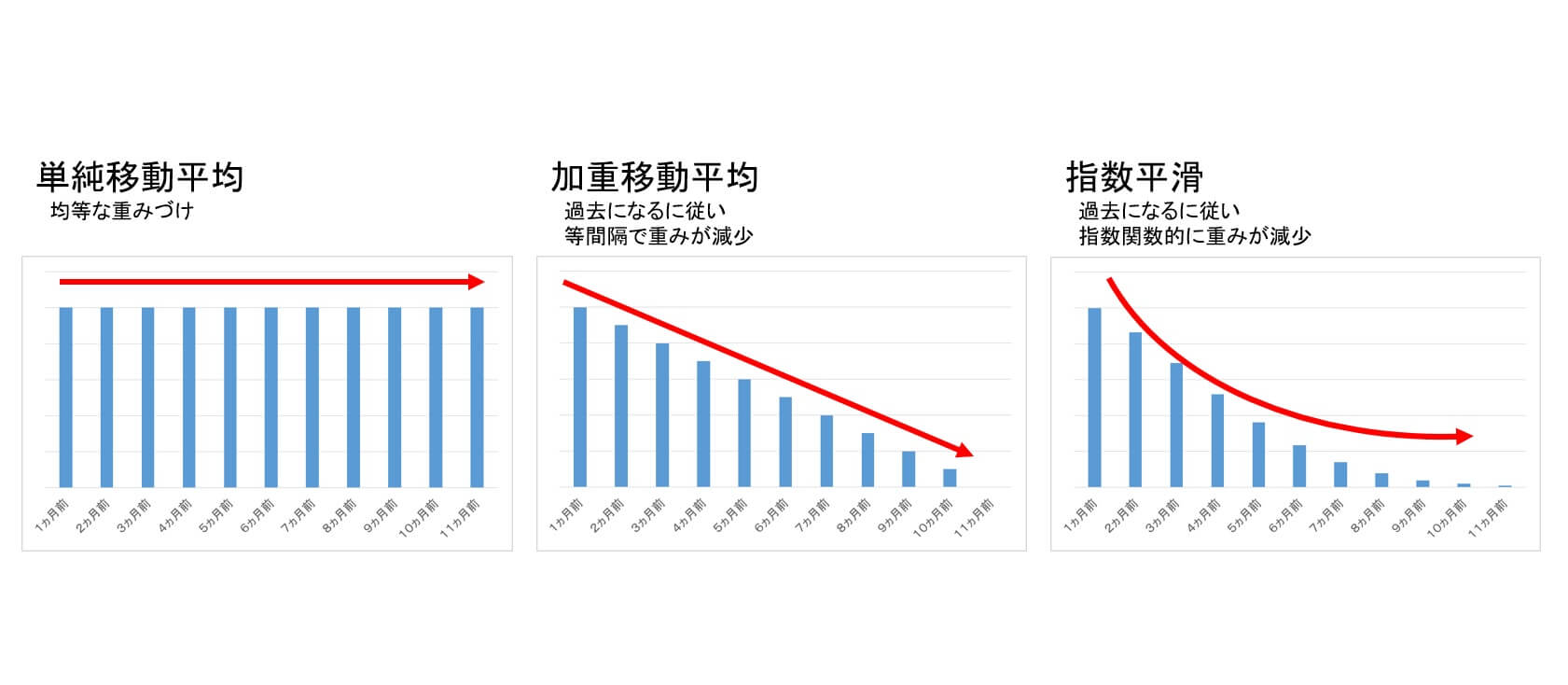
一次指数平滑法は、過去の実績データを用いつつ「より新しい方の実績値」により大きな重みを置き、過去になるほど小さな重みをかけて移動平均を算出する方法を指す。
過去に遡るほど、重みは指数関数的に減少するので「指数」平滑と呼ばれる。
今期の指数平滑値 = 前期の指数平滑値 + α係数(前期の実績値 – 前期の指数平滑値)
・α係数
平滑化定数αとは、上記計算式にあるとおり、過去データ重みづけのための係数。
0以上1以下の値を画面上に入力する。
αが1に近いほど直近のデータが重視され、αが0に近いほど過去のデータが重視される。
α係数最適化による一次指数平滑法
上記で紹介した一次指数平滑法について、α係数を手動で指定しせず自動最適化する場合に選択する。
最適化は、実績値と需要予測値の平均絶対偏差が最小化されるように算出される。
平均絶対偏差は、まず需要予測に用いる過去データの期間において、期毎に(実績値 - 予測値)の差の絶対値を取り、期間内の絶対差を総和して、それを期間数で割って初期値を求める。
その後、期毎の平均絶対偏差を指数平滑により求める。この時、平滑化係数として使用されるのがδ係数となる。
今期のMAD = δ係数 (今期実績値と今期予測値の差の絶対値) + (1 – δ)(前期のMAD)
単純移動平均法
単純移動平均法では、過去データの総和を期間数で単純に割った平均値を需要予測値とする。
過去データに対する重みづけはない。(10年前の実績も、直近の実績も同じ扱い)
よって、画面パラメータの入力値は履歴期間のみとなる。
加重移動平均法
加重移動平均では、過去データに対して重み付け(加重)を行って移動平均を求める。
過去に遡るほどに一定量ずつ荷重は減らしていく。
パラメータとしては「加重グループ」を指定する。
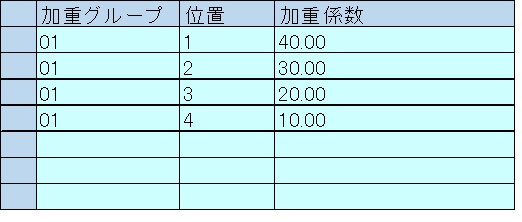
加重グループはカスタマイズで、以下で定義した係数により重みづけが決定される。
加重グループ(Tr:SPRO)
【生産計画/管理 >資材所要量計画 >需要予測 >加重グループ(加重移動平均)】
キー項目。
【位置】
係数をかける履歴地の位置。
1を指定すれば前期、2を指定すれば前々期を意味する。
【加重係数】
重みづけの係数を設定する。
季節傾向モデル
季節傾向モデルの一次指数平滑法(ウインターズ法)
ウインターズ法による需要予測は、季節によって変動する需要や、長期的な増加や減少傾向を需要予測値に反映させる。
ウインターズ法では、需要量を①基準値、②傾向値、③季節変動値の3要素で構成する。
具体的な計算式は以下の通り。
基準値、傾向値、季節変更値の計算は、それぞれ過去の実績を指数平滑化することで、今期の値を以下のように算出する。
今期の基準値 = α(今期の実績 ÷ 今期の季節変動値) + (1 – α)(前期の基準値 + 前期の傾向値)
今期の傾向値 = β(今期の基準値 – 前期の基準値) + (1 – β)(前期の傾向値)
今期の季節変動値 = γ(1周期前の実績 ÷ 1周期前の基準値) + (1 – γ)(1周期前の季節変動値)
このモデルを使用するときは、α・β・γそれぞれの係数と、1周期における期間数(通常は1年=12期)をパラメータとして入力する。
β係数はトレンド傾向に対する重みづけの指数平滑化係数で、同じくγ係数は季節変動に対する重みづけの指数平滑化係数となっている。
季節モデル
季節モデルの一次指数平滑法(ウインターズ法)
季節モデルは、季節による消費量の変動はあるもののトレンドの傾きが無い場合に適用する。
先述の季節傾向モデルから、傾向に関わる変数を取り除けば季節モデルとなる。
次期需要予測 = (今期の基準値) × (1周期前+1期の季節変動値)
今期の基準値 = α(今期の実績 ÷ 今期の季節変動値) + (1 – α)(前期の基準値)
今期の季節変動値 = γ(1周期前の実績 ÷ 1周期前の基準値) + (1 – γ)(1周期前の季節変動値)
手動設定するパラメータも、このモデルではβ係数の項目が存在せず、α係数・γ係数・季節期間のみ。
傾向モデル
トレンド(傾向)が見られる、つまり長期的に増加傾向、減少傾向のある場合には傾向モデルを適用する。
傾向モデルの一次指数平滑法(ウインターズ法)
先述の季節傾向モデルから、季節に関わる変数を取り除けば傾向モデルとなる。
今期の基準値 = α(今期の実績) + (1 – α)(前期の基準値 + 前期の傾向値)
今期の傾向値 = β(今期の基準値 – 前期の基準値) + (1 – β)(前期の傾向値)
画面入力のパラメータもα係数・β係数のみ。
二次指数平滑法
このモデルを選んだ場合、LES(Linear Exponential Smoothing)法による計算式が適用される。
計算式を以下の通り記述する。
なお、G1は一次指数平滑による基準値、G2は二次指数平滑により基準値、tは期間を表す変数とする。
G2(t) = α(G1(t)) + (1 – α)(G2(t-1))
予測値(t) = 2 × (G1(t) – G2(t)) + α(G1(t) – G2(t)) × (1 / (1 – α))
α係数最適化による二次指数平滑法
二次指数平滑法においてα係数を自動最適化する場合に適用するモデル。
最適化の方法については、一次指数平滑で説明した内容と同様。
初期化について
品目マスタ 需要予測タブの管理データの項目に「初期化」というフラグがある。
さりげない項目だがこれが重要で、初期化とは、需要予測計算の開始に必要な初期パラメータを求めるプロセスの事だ。
以下のウインターズ法の基準値の計算式を見てわかる通り、指数平滑法は今期の指数平滑を求めるために、前期の指数平滑値を前提としている。
しかし過去に遡っていると、どこかで実績データは無くなるので、その最も初回の期では基準値を求められないということになってしまう。そこで、計算を開始するための最初の値(初期値)が与えられる必要がある、その計算プロセスを「初期化」と呼ぶ。
初期化は正確な需要予測を行うために必要なプロセスなので、品目マスタの「初期化」には”X”を設定しておくことを推奨する。
初期化に必要な履歴期間
需要予測モデルごとに、初期化に必要な最低期間数が定められている。
初期化のプロセスを行うためには、一定期間の実績が存在する必要があるというわけだ。
モデルごとの必要期間数は以下の通り。
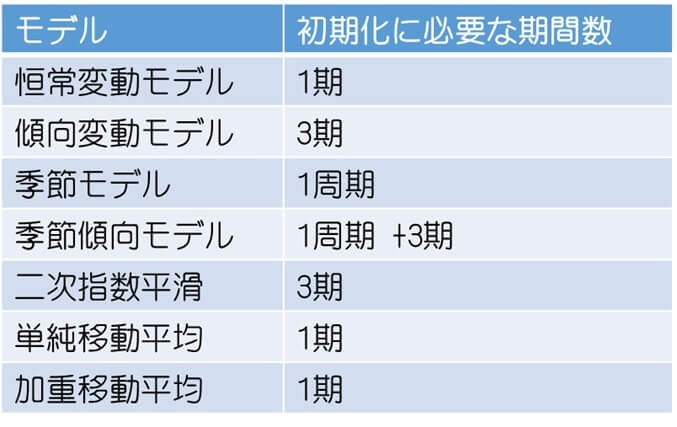
初期化期間数や期間範囲の設定により、予測結果が大きく変動する場合もよくあるので、それらパラメータ設定はよく吟味する必要がある。
指数平滑を用いたモデルを使用する場合は、1~2周期分の初期化期間があれば望ましい結果が得られる期待が高くなる。